Marlin固件中Bresenham算法与实现

本文最后更新于：2020年1月8日 凌晨

理论计算

Bresenhan算法将坐标系分割成棋盘形状，每个像素占有一个棋格，当我们进行采样时（直线斜率小于1），如下图所示，假设给定绘图的起始点为（10,11），那么绘制下一个采样点的坐标必然是从（11,11）和（11,12）中选择一个。如果把这种情况一般化，对于绘制直线的起始点是（Xk,Yk），那么其下一个采样点必然是（Xk+1,Yk）或者(Xk+1,Yk+1)中的一个。

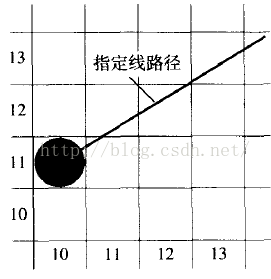
enter description here

那么该选择这两点中的哪一个点呢？选择更接近理论线路径的那个点。

enter description here

enter description here

想要得到3.16表达式，需要将yk=m*xk+b(一般直线方程)带入式3.14中，而且应该注意△y和△x都是常量，△y为给定的起始点和终点的纵坐标差的绝对值，△x为给定的起始点和终点的横坐标的差的绝对值。

注意：文中所说的p0是已经根据运动起点计算出的p值，它决定的是实际第一步的运动方向。许多文章也叫p1。

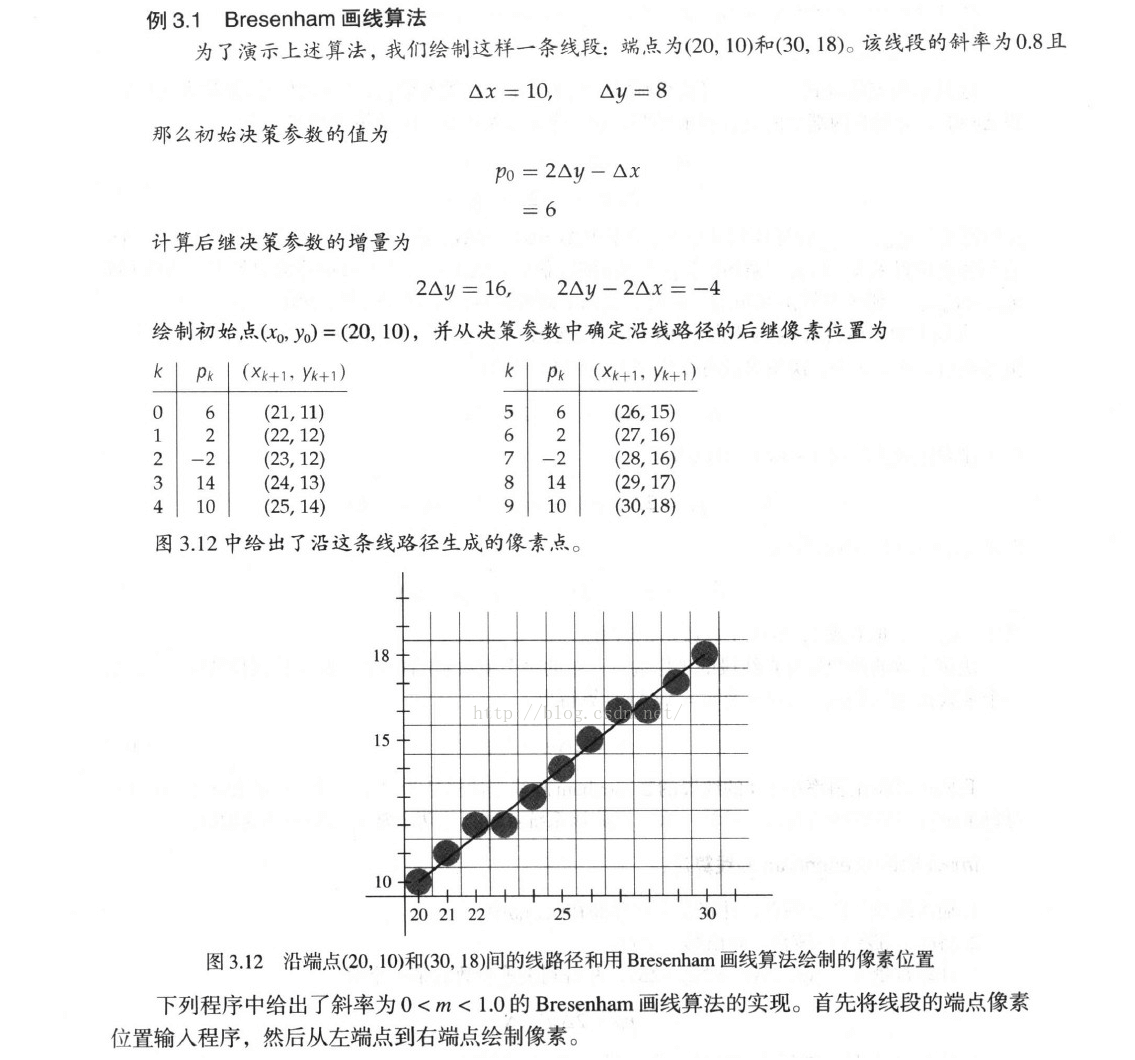
enter description here

enter description here

这里的△x实际是运动长度最长的那个轴总长度作为横坐标（上述默认X轴移动最长），△y是我们当前要移动的轴总长度，p也是依赖于当前轴的（上面默认p0 = py,实际还有px）

上图中是首先计算出p0,再判断p0决定第一步该怎么走，再对p进行计算，再判断，如此循环。注意这个判断和计算顺序。

代码实现

实际代码如下：

  • 我们不知道那个是最长轴，则p0是随着轴变化的，每个轴都需要单独计算
  • 默认 xEnd > x0,yEnd > y0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

void lineBresenham(int x,int y,int xEnd,int yEnd)
{

	int dx=xEnd-x0,dy=yEnd-y0;
    int dm = max(dx,dy)   // 取最长轴
	int px=2*dx-dm;   // p0x
    int py=2*dy-dm;   // p0y
	int counter = 0;  //  计算已经运动的步数，和最长轴对比看是否到达终点
    
	SetPixel(x,y);  // 画初始点
	while (counter<dm)
	{
		if(px>0){   // 这里如果我们假设x轴最长，则实际px始终大于0，则px就失去了意义
			x++;
			px+=2*dx-2*dm;
		}
        else
          px+=2*dx;	
          
        if(py>0){
			y++;
			p+=2*dy-2*dm;
		}
        else
          py+=2*dy;
          
        counter ++;
		SetPixel(x,y);  // 画点
	}
}

不知道你有没有发现无论p是正负，都需要计算 pk+1 = pk +Δy，只有在pk >0时，才再减去Δx。

但是再程序上你没法将它提取出来，这就很尴尬。而且若是提取出来只能放在 if 语句之前，那么问题来了，咋搞？

仔细分析你会发现问题出来p0上，因为我们在设置p0变量时就已经根据初始位置进行了一次预计算。如果我们这里将p0在往前推一次，你会发现一个很神奇的现象

  • p-1 = dm，它不依赖当前轴，即所有轴的p-1相同

然后将p0的计算并入到while循环中，此时再将上述程序优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

void lineBresenham(int x,int y,int xEnd,int yEnd)
{

	int dx=xEnd-x0,dy=yEnd-y0;
    int dm = max(dx,dy)   // 取最长轴
	int px = py =-dm
	int counter = 0;  //  计算已经运动的步数，和最长轴对比看是否到达终点
    
	SetPixel(x,y);  // 画初始点
	while (counter<dm)
	{
        px+ = 2*dx  // 在这里计算p0
		if(px>0){   // 这里如果我们假设x轴最长，则实际px始终大于0，则px就失去了意义
			x++;
			px- = 2*dm;
		}
        
        py+ = 2*dy
		if(py>0){
			y++;
			py- = 2*dm;
		}
      
        counter ++;
		SetPixel(x,y);  // 画点
	}
}

你会发现效果一样，只是更改了p0的计算位置，我们就可以将程序优化一部分。

再进一步变换一下想法，为了减少计算量，我们将所有的公式左右两边都除以2。则

  • 1/2p0 =Δy-1/2Δx

令p0 = 1/2p0，并不影响正负值判断。则：

  • p-1 =1/2Δx

  • pk <0：pk+1 = pk +Δy

  • pk >0：pk+1 = pk +Δy - Δx

到这里其实就和Marlin的程序基本是一致的了。

下面是Marlin的源程序，简化了一些并加了注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
void Stepper::isr() {
   
   // p-1 =1/2Δx 
   // step_event_count = dm 最长轴步数
    counter_X = counter_Y = counter_Z = counter_E = -(current_block->step_event_count >> 1);
    step_events_completed = 0;  //计算已经运动的步数，和最长轴对比看是否到达终点
    bool all_steps_done = false;  // 到达终点标志
  
    #define _COUNTER(AXIS) counter_## AXIS  // 每轴 pk 宏
    #define _APPLY_STEP(AXIS) AXIS ##_APPLY_STEP  // 驱动每轴step引脚，发出一个脉冲走一步
    #define _INVERT_STEP_PIN(AXIS) INVERT_## AXIS ##_STEP_PIN  // 脉冲方向，用户设定
    
    // 开始脉冲
    // steps[]是每轴的 dx/y/z
    #define PULSE_START(AXIS) \
      _COUNTER(AXIS) += current_block->steps[_AXIS(AXIS)]; \   // pk+1 = pk + dx
      if (_COUNTER(AXIS) > 0) { _APPLY_STEP(AXIS)(!_INVERT_STEP_PIN(AXIS),0); }

    // 停止脉冲，重置Bresenham计数器，更新位置
    #define PULSE_STOP(AXIS) \
      if (_COUNTER(AXIS) > 0) { \
        _COUNTER(AXIS) -= current_block->step_event_count; \  // pk+1- = pk+1 - 2*dm
        _APPLY_STEP(AXIS)(_INVERT_STEP_PIN(AXIS),0); \    // 停止脉冲
      }
     
     
     PULSE_START(X);  // 开始驱动
     PULSE_START(Y);
     PULSE_START(Z);
     PULSE_START(E);
     
     DELAY_NOPS(EXTRA_CYCLES_XYZE);  // 脉冲延时，一个脉短时间限制
     
     PULSE_STOP(X);
     ...
      
      if (++step_events_completed >= current_block->step_event_count) {
            all_steps_done = true;
             break;
    }
}

参考文档

01-专业
Marlin固件中Bresenham算法与实现
http://lonlypan.com/2020/01/08/Marlin固件中Bresenham算法与实现/
作者
LonlyPan
发布于
2020年1月8日
许可协议